Experiments with differentiable rendering

Here I’ll share with you some of my favourite failures when developing the differentiable renderer.

Reconstructing test spheres from a RGB

In this experiment I tried fitting a Neural SDF to a single RGB image of two balls via a differentiable sphere marcher. This setup is called single view reconstruction (SVR) as we try to reconstruct the 3D shape of the object being provided with only a single image. The RGB values represent XYZ positions in the space, cut off to range [-1,1]. The model was supervised by a single pre-made RGB image to test the convergence of the rendering pipeline.

The neural SDF wasn’t correctly cut off by the back wall of the bounding spherical volume so the entire back of the network was visible. During training the entire back side of the network was optimized leading to no clear bounds of the object. The shakiness in this GIF is literally from shaking the virtual camera to get a better surface approximation for similar viewing angles.

The resulting image rendered in higher resolution shows beautiful patterns formed by this faulty rendering process.

However, when the network is viewed from a different direction it reveals new mesmerizing patterns. This image displays the state of my mind when the results were once again wrong.

Reconstructing test spheres from a silhouette

In this experiment I took a step back and tried reconstruct a shape using a silhouette image. Finally, I got promising results by optimizing only the scale and position of sphere centers.

Tweaking the network hyperparameters sometimes got wery wrong, such as this one where I deliberately increased the learning rate to see what happens. Still it is a very cool looking animation, like it transformed into a kind-of defensive configuration.

Reconstructing test airplanes

After I’ve succesfully fitted a sphere, I tried using a more detailed object such as an airplane. The initial results were wery twitchy because of a small network and large learning rate as seen in this GIFs of the silhouette predictions and its mean squared errors through the optimization steps.

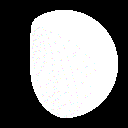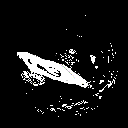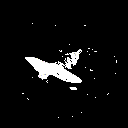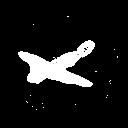
Finally, after increasing the network size reducing the learning rate quite a bit results became much more pleasing.